Inductive biases in Transformers
course project
Link to report Link to code Link to video
In this project, we investigate the nature of deep image priors in modern vision architectures like transformers and swin transformers by using methods introduced in “Deep Image Prior” by Ulyanov et al . This consists of using a randomly initialized neural network to perform certain reconstruction tasks like image denoising, image inpainting, super-resolution etc.
We find the following interesting results:
(a) Transformers have almost no inductive biases as compared to CNNs
(b) Swin Transformers do not have any better inductive biases as compared to vanilla Transformers when it comes to image reconstruction
(c) There are actually two kinds of inductive biases: predictive inductive biases (useful for learning an input to output function) and generative inductive biases (useful for learning a generative model), convolutional layers have both but image reconstruction tasks only measure generative biases.
(d) Swin transformers have better predictive inductive biases but almost no generative inductive bias.




We can see that Transformers do a poor job of denoising the image as compared to SkipNets. The “denoised” image output by the Transformer is still very noisy as compared to SkipNet’s denoised image. Similarly, SkipNet’s inpainting is almost flawless, with hardly any artifacts visible while the Transformer inpainting is very poor, with multiple visible artifacts. We can also see faint grid lines on the image which are remnants of the patch boundaries of the transformer. Surprisingly, Swin transformers do not perform any better than transformers at these tasks, even though they have a hierarchichal architecture which is supposed to .
To analyze why even Swin transformers don’t work as expected, we first distinguish between two kinds of inductive biases present in models, generative biases and predictive biases. Generative bias is the bias towards generating a family of data distributions, while predictive bias is bias towards learning a particular family of input-output mapping. For example, for CNNs, shift invariance is an example of predictive bias, and not generative bias, since it is related to how the target (that is, the labels) is invariant to changes in the image. However, as we just described, convolutional layers also have generative biases, but these are very distinct from predictive biases. In general, generative inductive bias is not equivalent to or even correlated with predictive inductive bias.
As we saw, the experiments in the deep image prior paper only test for image reconstruction tasks, which are good for measuring generative biases but not predictive biases. The hierarchical nature of the Swin transformer induces favorable predictive inductive biases but not generative inductive biases. This could be one reason why they are used in many predictive tasks like image classification, segmentation, etc but not generative tasks where CNNs are still state of the art.
In order to test this, we can perform the following experiment. We can equip the transformer with a stack of convolutional layers, before the input of the transformer or after the output of the transformer. When equipped before the transformer, these convolutional layers induce favorable predictive inductive biases because these convolutional layers can be trained to identify input image features (like edges, corners, etc), but hardly any generative biases because they will be suppressed by the biases of the transformer which transformers the output of the convolutional layers. When equipped after the transformer, they will hardly contribute to predictive biases because the image structure in the input signal has been completely changed by the transformer, but they will induce good generative inductive biases. In some sense, this is similar to attaching a ConvNet decoder to the transformer, which inherits the favorable generative inductive biases of the decoder. According to the theory we outlined, a model with convolutional layers after the transformer output should be much better at image reconstruction as compared to a model with convolutional layers equipped before the transformer input.
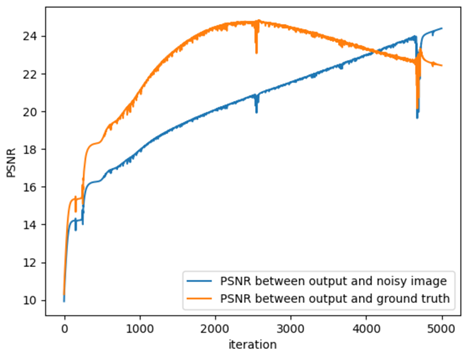
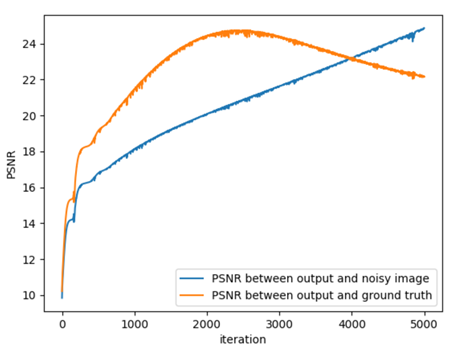
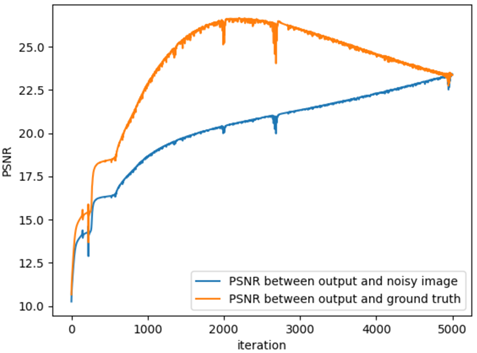
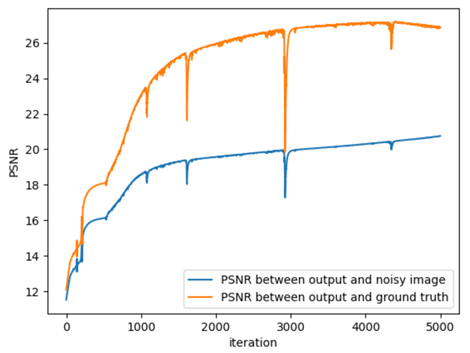
From left to right: (a) Plain transformer (b) 3 convolutional layers before a transformer (c) 1 convolutional layer after a transformer (d) 3 convolutional layers after a transformer
As we can observe, even adding 3 convolutional layers before the transformer does not really help, since the generative bias due to the convolutions is negligible. However, even adding one convolutional layer after the transformer really helps the gap between the PSNRs . Even after 4000 iterations, the gap between the PSNRs is still positive for the transformer with 1 convolutional layer, with higher max PSNR. Adding 3 conv layers after the transformer only helps more, as the gap is still high and positive even after 5000 iterations.
More details are there in the report and the the code